试题详情
- 简答题 设g(t)的频谱为G（ω）,求信号
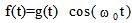的傅立叶变换。
-
因为：
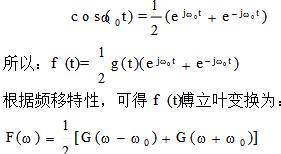
关注下方微信公众号，在线模考后查看
热门试题
- 拉普拉斯变换满足线性性。
- 用长除法求对应的时间序列，设其收敛域为|
- Z[2nu（n）]
- 证明
- e(t)与h(t)的卷积表达式为（）。
- 如果一个系统的幅频响应是常数，那么这个系
- 已知信号f（t）是因果信号其拉氏变换为，
- 与DFT相比，CTFT不适宜于在数字计算
- 根据定义求取单位冲击函数和单位阶跃函数的
- 信号时移只会对幅度谱有影响。
- 等于：（）
- 傅立叶变换与傅立叶逆变换的本质是一致的，
- 根据定义求序列的Z 变换，并且
- 信号可以分为连续信号和（）。
- nx（n）的Z变换结果是-zX（z）。
- 冲击信号的拉氏变换结果是一个常数。
- 时不变系统的响应与激励施加的时刻有关。
- Z[（-1）nu（
- 某个序列的ZT有2个极点-2，-4，请指
- 所有高于截止频率的频率分量都将不能通过系