试题详情
简答题某个股票现价为$50。已知在6个月后，股价将变为$60或$42。无风险年利率为12％（连续复利）。计算执行价格为$48，有效期为6个月的欧式看涨期权的价值为多少。试计算分析无套利原理和风险中性估价原理能得出相同的答案。
  • 6个月后期权的价值为$12（当股价为$60时）或$0（当股价为$42时）。
    考虑如下资产组合：
    ＋Δ份股票
    －1份看涨期权
    则资产组合价值为60Δ－12或42Δ。
    当60Δ－12＝42Δ，即Δ＝0.67时，
    6个月后，无论股价如何变化，该资产组合的价值将均为$28；此时组合的Δ
    值是无风险的。组合的现值为：50Δ－f
    其中f为期权的价值。
    （1）根据无套利原理，该资产组合必须是无风险的，因而有：

    则有：f＝6.96
    （2）根据风险中性估价定理，设p为风险中性条件下股价上升的概率，有：

    即：p=0.6162
    在风险中性世界，期权的期望价值为：
    12×0.6162＋0×0.3838＝7.3944
    其现值为：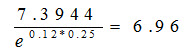
    所以，无套利原理与风险中性估价定理的计算结果一致。

  • 关注下方微信公众号，在线模考后查看

热门试题