试题详情
- 简答题 以X表示某种小包装糖果的重量(以g计),设
 今取得样本(容量为n=10):
今取得样本(容量为n=10): 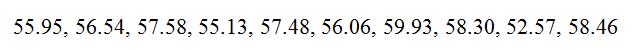 (1)求μ的最大似然估计值。 (2)求μ的置信水平为0.95的置信区间。
(1)求μ的最大似然估计值。 (2)求μ的置信水平为0.95的置信区间。
-

关注下方微信公众号,在线模考后查看

热门试题
- (1)一条绳子长为2l,将它随机地分为两
- 设(X,Y)的联合概率密度为
- 一批零件中有9个合格品与3个废品.安装机
- 设随机变量(X,Y)的联合分布密度函数是
- 一个袋内装有大小相同的7个球,其中4个是
- 把长为a的棒任意折成三段,求它们可以构成
- 设X,Y是两个相互独立的随机变量,X在(
- 一箱产品共100件,其中次品个数从0到2
- 已知随机变量X服从参数为λ的泊松分布,且
- 设随机变量X的概率密度为,现对X进行四次
- 若函数是某个连续随机变量X的概率密度,则
- 一批晶体管共40只,其中3只是坏的,今从
- 设随机变量X服从参数为2的指数分布。证明
- 设总体X服从二项分布B(2,0.3),为
- 设随机变量X和Y相互独立,且都服从正态分
- 设A、B互为对立事件,且,则下列各式中错
- 设随机变量X与Y的期望和方差存在,且D(
- 设随机变量X的概率分布为则EX
- 在一家保险公司里有10000人参加保险
- 设随机变量X的概率密度函数为是X的分布函