试题详情
- 简答题
描述一线性时不变因果连续时间系统的微分方程为
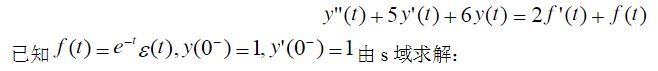零输入响应yx（t）零状态响应yf（t），完全响应y（t）；
-
关注下方微信公众号，在线模考后查看
热门试题
- 已知信号x（t）=u（t+1）-u（t-
- 全通系统的H（S）对零极点分布的要求为（
- 一个离散LTI系统的网络函数H（z）的极
- 周期信号的频谱是离散谱，非周期信号的频谱
- 系统的零输入响应等于该系统的自由响应。
- 离散时间系统，系统函数收敛域∞≥∣z∣＞
- 某离散时间系统的差分方程为a0y（n+2
- 分别绘出下列各序列的图形。 (1)x[n
- 若周期信号f（t）是奇谐函数，则其傅氏级
- 绘出下列时间函数的波形图: f
- 强迫响应一定是稳态响应。（）
- 象函数F（S）=的逆变换f（t）为（）
- 若系统的零状态响应y（t）=f（t）*h
- 如图所示z域框图，尝试写出其差分方程。
- 设信号f（t）的频谱F（ω）
- 绘出序列的图形。
- 下列信号中为非周期信号的是（）
- 已知H（s）的零、极点分布图如示，并且h
- 某LTI连续系统的输入信号为f(t)=e
- 若已知F[f(t)]=F(j&Omega