试题详情
- 简答题 设初值问题y′=x2+100y,y(0)=0, (a)由Euler方法、取步长h=0.1写出表示上述初值问题数值解的公式; (b)由改进Euler方法、取步长h=0.1写出上述初值问题数值解的公式。
-
如下:
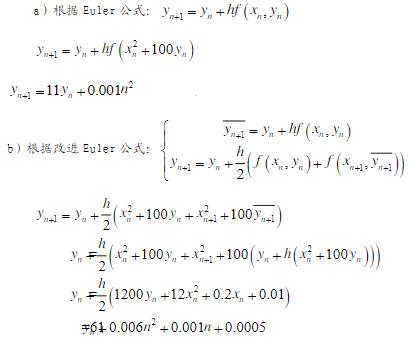
关注下方微信公众号,在线模考后查看

热门试题
- 设函数f(x)由下表给出:
- 设x=(3,-1,5,8)T<
- 设An-1是由豪
- 用带位移的QR方法计算 全部特征值。
- 已知f(-1)=2,f(1),f(2)=
- 如有下列表函数: 试计算此列表函数的差
- 对于n+1个节点的插值求积公式至少具有(
- 证明两点三次埃尔米特插值余项是 并由此求
- ,则A的谱半径ρ(A)=(),A
- 设(1)方程f(x)=0有根x*: (2
- 有下列数表: 所确定的插值多项式的次数
- 证明:如果A是正交阵,则cound(A)
- 设求方程f(x)=0的根的牛顿法收敛,则
- 用改进的Euler法解初值问题取步长h=
- 牛顿插值多项式的余项是()
- 直接推导出2步Adams显式公式
- 写出梯形公式和辛卜生公式,并用来分别计算
- 构造求解方程ex+
- 用列主元消元法解线性方程组作第一次消元后
- 设矩阵的A=LU,则U=()。