试题详情
- 简答题甲袋中有N-1只白球和一只黑球，乙袋中有N只白球，每次从甲，乙两袋中分别取出一只球并交换放入另一袋中去，这样经过了n次，问黑球出现在甲袋中的概率是多少？并讨论n→∞时的情况。
-
设An={经n次试验后，黑球出现在甲袋中}，
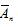={经n次试验后，黑球出现在乙袋中}，Cn={第n次从黑球所在的袋中取出一个白球}。记
时，由全概率公式可得递推关系式：
初始条件p0=1，由递推关系式并利用等比级数求和公式得
关注下方微信公众号，在线模考后查看
热门试题
- 点估计常用的两种方法是：（）和（）.
- 从一批炒股票的股民一年收益率的数据中随机
- 设一批产品中一、二、三等品各占60%，3
- 某维尼龙厂根据长期正常生产积累的资料知道
- 设随机变量X服从泊松分布，若EX
- 从学校乘汽车到火车站的途中有3个交通岗，
- 设随机变量X的密度函数为， 求E（X），
- 设X1,X
- 设随机变量X的概率密度为 求随机变量函
- 从5副不同的手套中任意取4只手套，求其中
- 50只铆钉随机地取来用在10个部件上，其
- 装有10件某产品（其中一等品5件，二等品
- 设总体X具有概率密度参数θ未
- 设总体X的分布律为： 其中0<θ<1/
- 若X~N（1,1），记其密度函数为f(x
- 设二维随机变量（X，Y）在抛物线y=x
- 设总体ξ~N(5,62<
- 设X1，X
- 设X表示连续抛两颗骰子，记事件A=“点数
- 假定人的脉搏服从正态分布，正常人的脉搏平