试题详情
简答题解释：群、交换群、有限群、有限群的阶、循环群、生成元、域、有限域、不可约多项式。
  • 群由一个非空集合G组成，在集合G中定义了一个二元运算符“· ”，满足： 
    （1） 封闭性：对任意的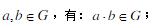
    （2） 结合律：对任何的
    （3） 单位元：存在一个元素1∈G（称为单位元），对任意元素，有：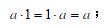
    （4） 逆元：对任意a∈G，存在一个元素a-1（称为逆元），使得：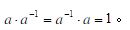
    如果一个群满足交换律，则称其为交换群。 
    如果一个群的元素是有限的，则称该群为有限群。 
    有限群的阶就是群中元素的个数。 
    如果群中每一个元素都是某一个元素a∈G的幂ak∈G（k为整数），则称该群是循环群。 
    在循环群中，认为元素a生成了群G，或a是群G的生成元。 
    域是由一个非空集合F组成，在集合F中定义了两个二元运算符：“+”（加法）和“· ”（乘法），并满足： 
    （1）F关于加法“+”是一个交换群；其单位元为“0”，a的逆元为-a 
    （2） F关于乘法“· ”是一个交换群；其单位元为“1”，a的逆元为a-1。 
    （3）（分配律）对任何的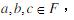
    （4）（无零因子）对任意的则a=0或b=0。 
    如果域F只包含有限个元素，则称其为有限域。 
    不可约多项式是指不能再分解为两个次数低于该多项式最高次的多项之积的多项式。

  • 关注下方微信公众号，在线模考后查看

热门试题