试题详情
- 简答题根据自由电子近似下的量子导电理论解释：准连续能级、能级的简并状态、简并度、能态密度、k空间、等幅平面波和能级密度函数。
-
准连续能级 ：电子的本征能量是量子化的，其能量值由主量子数n决定，并且其能量值也是不连续的，
能级差与材料线度L²成反比，材料的尺寸越大，其能级差越小，作为宏观尺度的材料，其能级差几乎趋于零，电子能量可以看成是准连续的。
能级的简并状态 ：把同一能级下具有多种能态的现象称为能级的简并状态。
简并度 ：把同一能级下的能态数目称为简并度。
能态密度 ：对于某一个电子体系，在k空间内单位体积内能态的数量或倒易节点数称为波矢能态密度。ρ =V/（2π）³，含自旋的能态密度应为2ρ
K.空间 ：如果使用波矢量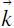
的
三个分量为单位矢量构筑坐标系，则每个能态在该坐标中都
是一个整数点，对于准连续的能级，此坐标系中的每个整数点都代表一个能态。人们把此坐标系常数称为k空间或状态空间。
等幅平面波 ：量子导电理论中在自由电子近似下用来描述电子运动行为的本征波函数，其波幅保持为常数。
能级密度函数 ：电子的波矢能态函数对其能量的分布函数，可以认为是在单位能量宽度上的能态分布，表达式为：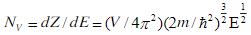
关注下方微信公众号，在线模考后查看
热门试题