试题详情
- 简答题 游客乘电梯从电视塔底层到电视塔顶层观光.电梯于每个整点的第20分钟从底层起行.假设一游客在上午八点的第X分钟到达底层候梯处,且X在[0,60]上均匀分布,记Y为该游客的等候时间。 (1)写出Y与X的函数关系; (2)不求Y的概率分布,直接利用(1)的结果求游客的等候时间的期望。
-
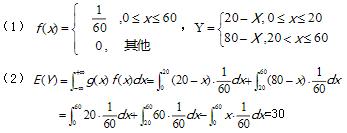
关注下方微信公众号,在线模考后查看

热门试题
- 设二维随机变量(X,Y)的联合概率密度为
- 设二维随机变量(X,Y)的联合分布函数为
- 设总体X服从均值为1/2的指数分布,X<
- 设总体X的概率密度为,是来自X的简单随机
- 一大楼装有5个同类型的供水设备,调查表明
- 设随机变量X的分布函数为 则a=(),
- 假设一大型设备在任何长为t的时间内发生故
- 设X1,X
- 有甲、乙两种味道和颜色极为相似的名酒各4
- 一公司向M个销售点分n(n〈M)发张提货
- 5人在第一层进入八层楼的电梯,假如每人以
- 设某工人连续生产了4个零件,表示他生产的
- 已知甲、乙两箱装有同种产品,其中甲箱中装
- 已知事件A发生必导致事件B的发生,且0<
- 设的N个袋子,每个袋子中将有a只黑球,b
- 若Cov(X,Y)=0,则下列结论中正确
- 设随机向量(X,Y)的联合分布密度为,则
- 若P(A)=0.5,P(B)=0.4,P
- 对于二维正态随机变量(X,Y),若ρ=1
- 设随机变量X在区间[1,2]上服从均匀分