试题详情
简答题 家用电器维修店只有一名维修人员，前来修理家用电器的顾客到达服从泊松分布，平均每小时4人。修理时间服从指数分布，修理一台家电平均需要6分钟。试求： （1）修理店闲时和忙时的概率； （2）平均队长和排队长； （3）平均等待时间和平均逗留时间。
  • 属于M/M/1排队模型，λ=5，μ=60/6=10，服务强度ρ=λ/μ=5/10=0.5
    （1）接待窗口处于忙时的概率1-ρ0=ρ=0.5，接待窗口处于闲时的概率ρ0=1-ρ=0.5
    （2）平均队长L=ρ/（1-ρ）=1人，平均排队长Lq=L-ρ=1-0.5=0.5人
    （3）平均逗留时间W=1/（μ-λ）=1/（10-5）=0.2小时

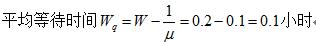
  • 关注下方微信公众号，在线模考后查看

热门试题