试题详情
- 简答题 设总体X的概率密度为 X1,X2,...Xn是取自该总体的一组简单随机样本,X1,X2,...Xn为样本观测值. (1)求参数λ的最大似然估计量 (2)你得到的估计量是不是参数λ的无偏估计,请说明理由
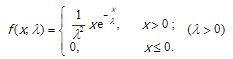
-
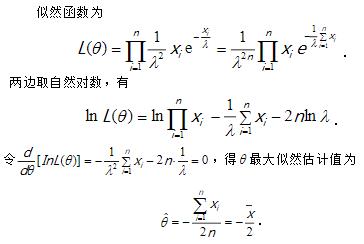
关注下方微信公众号,在线模考后查看

热门试题
- 设某种电灯泡的寿命X服从指数分布,从中抽
- 设总体服从参数为1/Θ的指数分布,若X为
- 从数字1,2,…,10中有放回地任取4个
- 已知三个随机变量X,Y,Z中,E(X)=
- X,Y相互独立,且都服[0,1]上的均匀
- A,B,C三人在同一办公室工作,房间有三
- 将一枚硬币连抛两次,则此随机试验的样本空
- 设某校女生的身高服从正态分布,今从该校某
- A,B,C三人在同一办公室工作,房间有三
- 测定家庭中的空气污染。令X和Y分别为房间
- 在电源电压不超过200V、200V~2
- 某工厂有甲、乙、丙三个车间生产同一种产品
- 比较两种枪弹的速度(均为正态分布,单位:
- 某保险公司的调查表明,新保险的汽车司机中
- 同时掷3枚均匀硬币,则恰有2枚正面朝上的
- 从1,1,2,3,3,3,4,4,5,6
- A,B,C是任意事件,在下列各式中,不成
- 设X1,X
- 设A,B,C三个事件两两独立,则A,B,
- 设A、B是Ω中的随机事件,则A∪B=A∪