试题详情
- 简答题
已知如图所示的三角形单元，设其厚度为t，弹性模量为E，泊松比为μ，三角形单元的结点坐标如图所示。
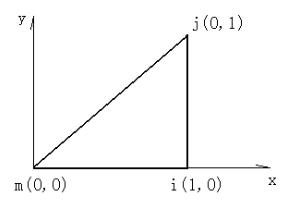求当νj=-1，ui=νi=uj=um =νm=0时单元的应力分量。
-
关注下方微信公众号，在线模考后查看
热门试题
- 为什么在主要边界（大边界）上必须满足精确
- 试写出无体力情况下平面问题的应力分量存在
- 厚壁圆筒内径为a，外径为b，厚壁圆筒内承
- 试分析说明，在板面上处处受法向约束且不受
- 试考察应力函数 能满足相容方程，并求出
- 连续性假定是指整个物体的体积都被组成这个
- 平衡方程反映了（）和（）之间关系的方程。
- 已知弹性实体中某点在x和y方向的正应力分
- 试利用应力转轴公式和胡克定律推导轴对称问
- 试证能满足相容方程，并考察它在下图所示矩
- 已知如图所示悬挂板，在O点固定，若板的厚
- 如图所示为一个桁架单元，端点力为[U1，
- 如何由单元刚度矩阵组建整体刚度矩阵（叠加
- 证明：如果体力分量虽然不是常量，但却是有
- 试比较极坐标和直角坐标系的平衡微分方程、
- 简述单元刚度与哪些因素有关。
- 梯形横截面墙体完全置于水中，如图所示。已
- 设有一边长为a的正方形截面杆，与一面积相
- 试求物体的刚体位移，即应变为零时的位移分
- 已知直角六面体的长度h比宽度和高度b大的