试题详情
简答题（投票博弈）假定有三个参与人（1、2和3）要在三个项目（A、B和C）中选中一个。三人同时投票，不允许弃权，因此，每个参与人的战略空间Si=（A，B，C）。得票最多的项目被选中，如果没有任何项目得到多数票，项目A被选中。参与人的支付函数如下：U1（A）=U2（B）=U3（C）=2U1（B）=U2（C）=U3（A）=1U1（C）=U2（A）=U3（B）=0求解以上博弈的所有纯战略纳什均衡。
  • 首先，将上述博弈过程转换为战略式博弈矩阵。

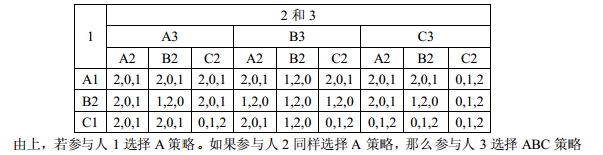
    1 选择 A 策略。如果参与人 2 同样选择 A 策略，那么参与人 3 选择 ABC 策略是无差异的。

  • 关注下方微信公众号，在线模考后查看

热门试题