试题详情
简答题 材料：如图所示，相邻四点连成的小正方形面积为1平方厘米。 （1）分别连接各点，组成下面12个图形，你发现有什么排列规律？ （2）求出各图形外面一周的点子数、中间的点子数以及各图形的面积，找出一周的点子数、中间的点子数、各图形的面积三者之间的关系。 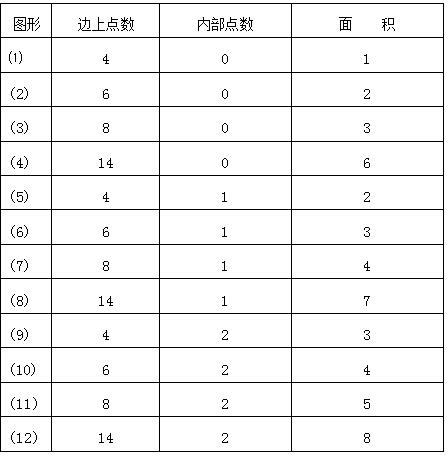利用所给材料，请你设计一个“数形结合”教学片断。
  • （一）、列表分析（也可以只列举部分图形分析）
    （二）、观察、归纳：（限于篇幅只列举部分图形分析）
    图形（1）的面积：4÷2＋0－1=1
    图形（3）的面积：8÷2＋0－1=3
    图形（5）的面积：4÷2＋1－1=2
    图形（8）的面积：14÷2＋1－1=7
    图形（9）的面积：4÷2＋2－1=3
    图形（11）的面积：8÷2＋2－1=5
    图形（12）的面积：14÷2＋2－1=8
    （三）、总结规律：
    图形的面积与格点数满足关系：面积＝边上的点数÷2＋内部点数－1
    （四）、教学设计
    一、找图的排列规律
    师：同学们看图，找出图的排列规律来。（学生可以讨论）
    生：老师我们发现，第一行的图中间没有点，第二行的图中间有一个点，第三行的图中间有两个点。
    师：非常好！
    二、数一数每个图周边的点数
    师：现在我们来数一数每个图周边的点数。并将结果填入下列表中。（师生一起数）
    三、计算面积
    师：数完边点数，我们再来计算每个图的面积。结果也填入表中。（师生一起计算）

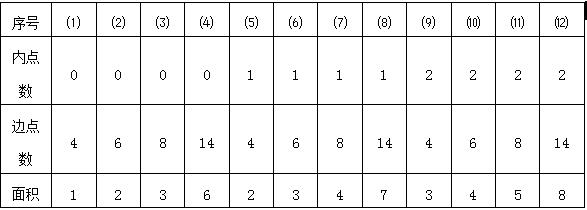
    四、寻找每一列三个数之间的规律
    师：我们根据这个表，找一找每列三个数之间的关系。告诉同学们，希望找到相同的规律。
    生：第一列，边点数等于面积乘以4。
    师：这个规律能否用到第二列呢？
    生：不能，因为6不等于2乘以4。
    生2：第一列，边点数除以2，减去面积等于1。
    师：好！看看这个规律能否用到第二列？
    生：能。还能用到第三、第四列。
    生2：老师，这个规律不能用到第五列。
    师：很好！我们看看这个规律到第五列可以怎样改一改。
    生：我发现了，边点数除以2，加上内点数，再减去面积等于1。
    师：非常好！大家一起算一算，是不是每一列都具有这个规律。
    五、总结
    师：我们把发现的规律总结成公式：边点数/2＋内点数－面积＝1
    也可以写为：边点数/2＋内点数－1＝面积

  • 关注下方微信公众号，在线模考后查看

热门试题