试题详情
- 简答题 试列出下列两图所示问题的全部边界条件。在其端部边界上,应用圣维南原理列出三个积分的应力边界条件。

-
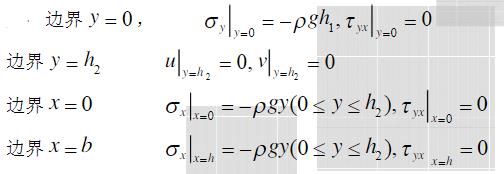
关注下方微信公众号,在线模考后查看

热门试题
- 试列出下列两图所示问题的全部边界条件。在
- 薄壁杆件承受扭矩T的作用,若杆件壁厚均为
- 已知复位势函数φf
- 试写出无体力情况下平面问题的应力分量存在
- 为了保证解答的收敛性,单元位数模式必须满
- 三角形常应变单元的特点是什么?矩形单元的
- 有限元法有哪些优缺点?
- 图示矩形弹性薄板,沿对角线方向作用一对拉
- 试导出轴对称位移问题中,按应力求解时的相
- 矩形截面柱体承受偏心载荷作用,如果不计柱
- 几何方程是研究()和()之间关系的方程。
- 试证明,如果体力虽然不是常量,但却是有势
- 弹性力学问题的方程个数有()个,未知量个
- 按应力求解平面问题,最后可以归纳为求解一
- 已知受力物体内某一点的应力分量为:,试求
- 在选择多项式位移模式的阶次时,要求所选的
- 诉述有限元法的定义。
- 试用虚位移原理求图示简支梁的挠曲线,并求
- 简述平面钢架问题有限元法的基本过程。
- 证明应力函数φ=axy能满足相容