试题详情
- 简答题 设Ax=b,其中A为非奇异阵。 (a)求证ATA为对称正定阵; (b)求证cound(ATA)2=(cound(A)2)2。
-
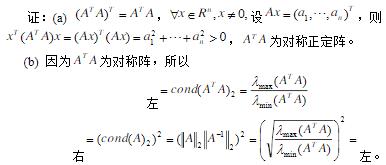
关注下方微信公众号,在线模考后查看

热门试题
- 用列主元消去法解线性方程组,第1次消元,
- ,则=(),A的谱半径ρ(A)=
- 下列方程组Ax=b,若分别用J法及GS法
- 分别用2.718281,2.718282
- 确定下列公式中的待定参数,使其代数精度尽
- 设An-1是由豪
- 已知sinx区间[0.4,0.8]的函数
- 用下列方法计算积分比较结果 (1)龙贝格
- 已知: 分别用拉格朗日插值法和牛顿插值
- 已知,求Householder阵H使Hx
- f(x)=x7+x
- 设x=(1,9,-5,2)T<
- 计算球体积要使相对误差限为1%,问度量半
- 取步长h=0.2,用预估-校正法解常微分
- 设 计算A的条件数。cound(A)<
- 用雅可比方法计算 的全部特征值及特征向
- 设数据x1,x
- 若则矩阵A的谱半径ρ(A)=()
- 等距二点求导公式f′(x1)≈()
- 设A与B为n阶矩阵,A为非奇异,考虑解方