试题详情
简答题 考虑一个全同原子组成的平面方格子，正方形的边长为a，每个原子的质量为M，最近邻原子的力常数为β。用ul，m记第l列，第m行的原子垂直于格点平面的位移。 （1）证明运动方程为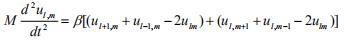： （2）设解的形式为 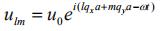， 证明色散关系为 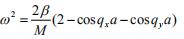。 （3）证明独立解存在的区域为边长为2π/a的正方形区域的正方形，分别画出q=qx，qy=0，和qx=qy时的ω（q）图。 （4）对于长波长极限，qa<<1时，证明 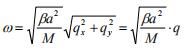（5）在第一布里渊区画出等ω线，并标出ω的极大值点，极小值点和鞍点。

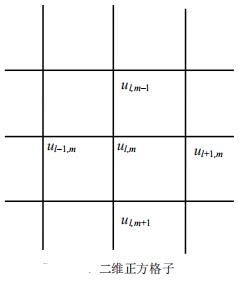
  • （1）对于（l，m）处原子，（l，m）处原子相对右边（l+1，m）处原子的相对位移为ul+1，m-ul，m，
    （l，m）处原子相对左边（l-1，m）处原子的相对位移为ul，m–ul-1，m，
    （l，m）处原子相对下边（l，m+1）处原子的相对位移为ul，m+1-ul，m，
    （l，m）处原子相对上边（l，m-1）处原子的相对位移为ul，m-ul，m–1，
    总的合力为：

  • 关注下方微信公众号，在线模考后查看

热门试题