有一离散无记忆信源，其输出为X∈{0，1，2}，相应的_睦霖题库

简答题有一离散无记忆信源，其输出为X∈{0，1，2}，相应的概率为p₀=1/4，p₁=1/4，p₂=1/2，设计两个独立的实验去观察它，其结果分别为Y₁∈{0，1}，Y₂∈{0，1}，已知条件概率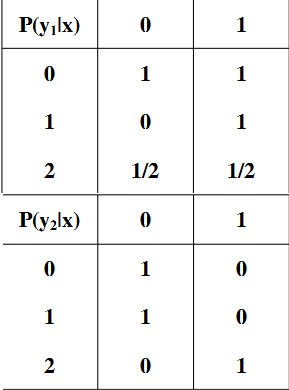：（1）求I（X；Y₁）和I（X；Y₂），并判断哪一个实验好些（2）求I（X；Y₁Y₂），并计算做Y₁和Y₂两个实验比做Y₁和Y₂中的一个实验可多得多少关于X的信息（3）求I（X；Y₁|Y₂）和I（X；Y₂|Y₁），并解释它们的含义

正确答案：
答案解析：
关注下方微信公众号，在线模考后查看

热门试题