试题详情
简答题两个兄弟分一块冰激凌。哥哥先提出一个分割比例，弟弟可以接受或拒绝，接受则按哥哥的提议分割，若拒绝就自己提出一个比例。但这时候冰激凌已化得只剩1/2了，对弟弟提议的比例哥哥也可以接受或拒绝，若接受则按弟弟的建议分割，若拒绝冰激凌会全部化光。因为兄弟之间不应该做损人不利己的是，因此我们假设接受和拒绝利益相同时兄弟俩都会接受。求该博弈的子博弈完美纳什均衡。
  • 假设哥的方案是S1：1-S1，其中S1是自己的份额，弟的方案是S2：1-S2，S2是哥的份额，那么可用如下的扩展形表示该博弈：

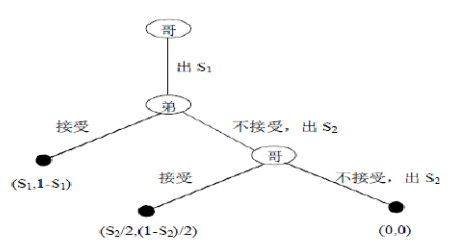
    运用逆推归纳法先分析最后一阶段哥的选择。由于只要接受的利益不少于不接受的利益哥就会接受，因此在这个阶段只要弟的方案满足S2/2≥0，也就是S2≥0，哥就会接受，否则不会接受。由于冰激凌的份额不可能是负数，也就是说因为哥不接受弟的方案冰激凌会全部化掉，因此任何方案哥都会接受。
    现在回到前一阶段弟的选择。由于弟知道后一阶段哥的选择方法，因此知道如果不接受前一阶段哥提出的比例，自己可以取S2=0，独享此时还未化掉的1/2块冰激凌；如果选择接受前一阶段哥的提议，那么自己将得到1-S1，显然只要1-S1≥1/2，即S1≤1/2，弟就会接受哥的提议。
    再回到第一阶段哥的选择。哥清楚后两个阶段双方的选择逻辑和结果，因此他在这一阶段选择S1=1/2，正是能够被弟接受的自己的最大限度份额，超过这个份额将什么都不能得到，因此S1=1/2是最佳选择。
    综上，该博弈的子博弈完美纳什均衡是：哥哥开始时就提议按（1/2，1/2）分割，弟弟接受。

  • 关注下方微信公众号，在线模考后查看

热门试题