试题详情
- 简答题系统的微分方程为
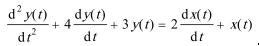， 初始状态为y'(0-)=4，u(0-)=1。若激励为x(t)=e-2tu(t) 。 （ 1 ）试用拉氏变换分析法求全响应； （ 2 ）分别求零输入响应和零状态响应，然后叠加得全响应。
关注下方微信公众号，在线模考后查看
热门试题
- 已知某离散信号的单边z变换为，求其反变换
- 极点和零点的意义是什么？它们有什么作用？
- 时限信号f（t）的收敛域是左半s平面。
- 表示离散系统的差分方程为： （1）求系统
- 有一幅度为1，脉冲宽度为2ms的周期矩形
- 如图所示RLC电路，已知：
- 象函数F（S）=的逆变换f（t）为（）
- 如果一线性时不变系统的单位冲激响应为h（
- 如题图示系统由加法器、积分器和放大量为a
- 已知某离散时间系统的输入f（n）和输出y
- 试计算下列结果。
- 已知f（t）的傅立叶逆变换为F（jω），
- 已知信号x（t）的傅里叶变换为X（jω）
- 给定系统微分方程为若激励信号与起始状态为
- 单位序列响应h（n）是指离散系统的激励为
- 画出系统函数，所表示的系统的级联和并联形
- 某一离散因果稳定线性时不变系统的单位序列
- 信号x（t）=3cos（4t+π/3）的
- 描述某系统的微分方程为y”（t）+4y’
- 由下列差分方程画出因果离散系统的结构图，