试题详情
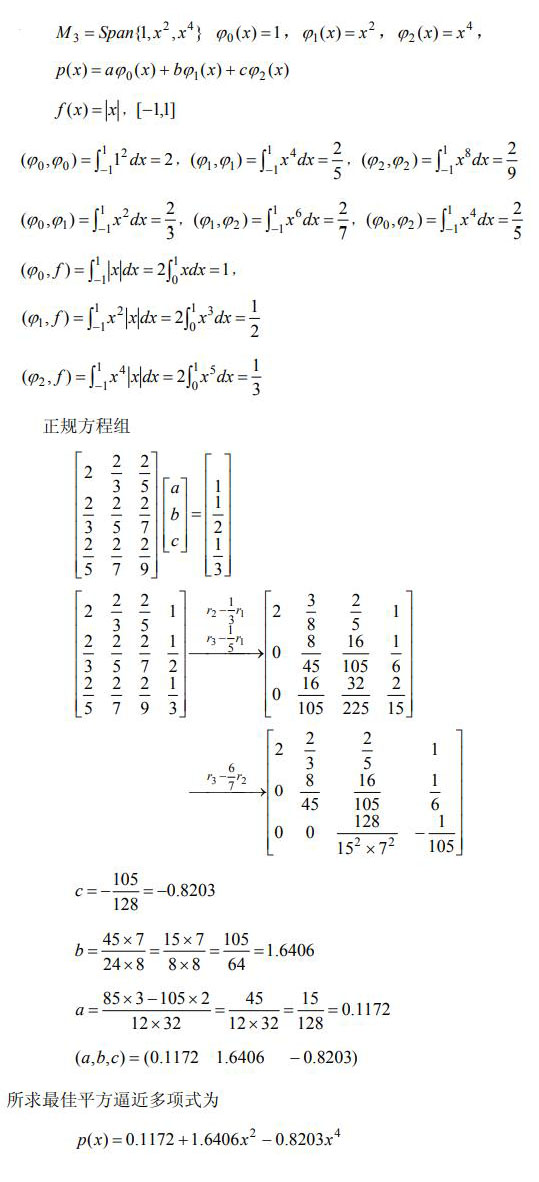
- 简答题设M3=Span{1,x2,x4},在M3中求f(x)=|x|在[-1,1]上的最佳平方逼近多项式。
关注下方微信公众号,在线模考后查看

热门试题
- 试推导矩阵A的Crout分解A=LU的计
- 已知a=1.2031,b=0.978是经
- 用追赶法求解三对角方程组
- 给定下列函数值表:
- 用辛普森公式求积分并计算误差
- 为了使计算的乘除法次数尽量地少,应将该表
- 设f(x)=C2[
- 方程求根的Newton法是如何推出的?它
- 设f(x)=4x5
- 试用Gauss消去法解下列方程组,计算过
- 求A、B使求积公式的代数精度尽量高,并求
- 用二分法求非线性方程f(x)=0在区间(
- 已知三角形面积,其中c为弧度,,且测量a
- 试建立一种收敛的Seidel迭代公式,说
- 数值积分公式的代数精度为()。
- 利用尤拉方法计算积分 在点x=0.5,1
- 设A为非奇异矩阵,求证
- φ(x)=x+a(x2
- 取≈1.732计算,下列方法
- 为求方程x3―x<