试题详情
简答题 设电子在无限深势阱中运动，势阱为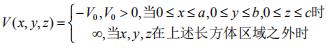： 求波函数和束缚态能级。
  • （1）在长方体区域内，V（r）=−V0，薛定谔方程化为：

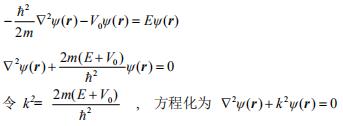
    这是一个三维偏微分方程，需要用分离变量法化为一微的微分方程组，根据分离变量的精神，令ψ（r）=X（x）Y（y）Z（z），如果解方程最后得到满足条件的一组解，那么满足薛定谔方程波函数的一般形式为这些解的线性组合。

    方程的左边为x的函数右边是y和z的函数，两个函数相等（这种相等的条件与自变量无关），必须是方程两边都等于一个常数，我们设这个常数为–kx2。

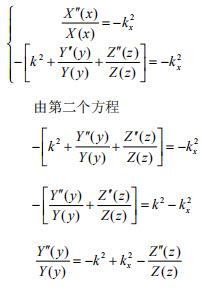
    方程的左边为y的函数右边是z的函数，方程两边要相等，必须有

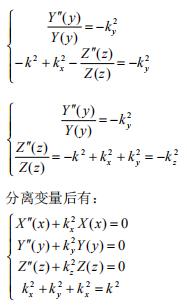
    自由电子薛定谔方程解的取法与边界条件密切相关。假定自由电子薛定谔方程满足周期性边界条件，方程将取平面波解。如果假定在边长为L的金属立方体外势能为无穷大，则方程的解取正弦余弦函数。于是有：

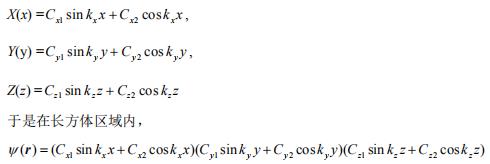
    （2）在长方体区域外，势能无穷大，波函数为0。
    在x=0的端面（平面）上，波函数连续，有：

    再根据归一化条件，计算积分：

  • 关注下方微信公众号，在线模考后查看

热门试题