试题详情
简答题完全竞争行业中某厂商的成本函数为TC=Q3-5Q2+20Q+50，成本以美元计算，假设产品价格为45美元。 （1）求利润最大时的产量及利润总额。 （2）如果市场需求发生变化，由此决定的新的价格为25.5美元，在新的价格下，厂商是否会发生亏损？如果亏损，亏损多少？ （3）该厂商在什么情况下停止营业？
  • （1）根据完全竞争厂商MR=MC利润最大化原则，求出利润最大化时的产量。
    S.TC=Q3-5Q2+20Q+50    MC=dTC/dQ=3Q2-10Q+20     P=MC=45
    3Q2-10Q+20=45   3Q2-10Q+20-45=0   3Q2-10Q-25=0   （3Q+5）（Q-5）=0   Q1=-5/3（舍）  Q2=5
    当Q2=5 时，利润（∏）=TR-TC=PQ-（ Q3-5Q2+20Q+50）= 45×5-（53-5×52+20×5+50）=75美元
    （2）当P=25.5时  根据P=MC  即 25.5=3Q2-10Q+20     Q1=3.81    Q2= -0.48（舍去）
    利润（∏）=TR-TC=PQ-（ Q3-5Q2+20Q+50）=25.5×3.81-（3.813-5×3.812+20×3.81+50）=－11.78美元     所以亏损
    （3） 当市场价格下降到P小于平均可变成本AVC， 即P≤AVC时，厂商必须停产。  因为TC=VC+FC    FC=50     所以VC=Q3-5Q2+20Q
    AVC=TVC/Q=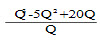=Q2-5Q+20
    对Q求导，令AVC/dQ=0    即2Q-5=0  Q=2.5时，  AVC达到最小值。
    把Q=2.5代入AVC   AVC=13.75     则，当市场价格P=13.75时，厂商必须停产。

  • 关注下方微信公众号，在线模考后查看

热门试题