试题详情
- 简答题平面上画有间隔为d 的等距平行线,向平面任意投掷一枚长为l(l<d)的针,求针与平行线相交的概率.
-

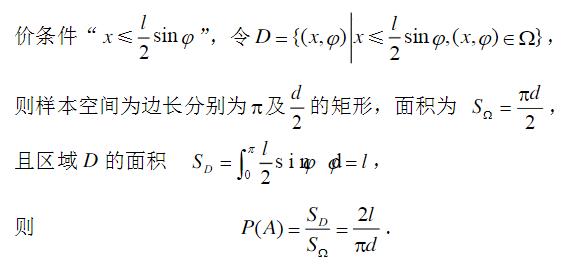
关注下方微信公众号,在线模考后查看

热门试题
- 用切比雪夫不等式估计下列各题的概率: (
- 一列火车共有n节车厢,有k(k≥n)个旅
- 5人在第一层进入八层楼的电梯,假如每人以
- 房间里有四个人,求至少两个人的生日在同一
- 甲、乙两个篮球运动员,投篮命中率分别为0
- 设随机变量X1,X
- 设总体X的分布律为 0<θ
- 设随机变量X的密度函数为 试求Y=si
- 设随机变量X的方差为2,则P{|X-E(
- 袋中有大小相同的红球4只,黑球3只,从中
- 设总体X的数学期望为μ,X1<
- X和Y是两个相互独立的随机变量,X在(0
- 对任意的随机事件A,B,C,试证:P(A
- 已知连续型随机变量X的概率密度函数为,求
- (1)设总体是来自X的样本是相应的样本值
- 设随机变量X分布律为 则P{1/2
- 某地抽样调查结果表明,考生的外语成绩(百
- 设正态总体的均方差σ=3,该
- 设总体X的密度函数为f(x,&theta
- 设随机变量X的密度函数为,求E(X),D