试题详情
- 简答题 已知在紧束缚近似下,面心立方晶体s态电子构成的能带为:
 (1)求能带宽度。 (2)求带低的有效质量。 (3)证明,在布里渊区中心,等能面近似为球形。并求布里渊区中心附近的有效质量。
(1)求能带宽度。 (2)求带低的有效质量。 (3)证明,在布里渊区中心,等能面近似为球形。并求布里渊区中心附近的有效质量。
-
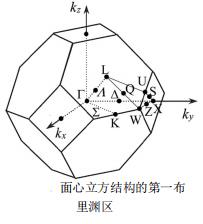
在kΓ=0处,E(k)取最小值
Emin=Es‒J0‒4J1(1·1+1·1+1·1)=Es‒J0‒12J1
在布里渊区W点,E(k)取最大值此时

关注下方微信公众号,在线模考后查看

热门试题
- 已知由N个同种金属原子构成的一维单原子
- 对于原子间距为a的同种原子构成的二维密
- 磁晶的各向异性
- 计算由N个质量为M的相同原子组成一维单原
- n型半导体是在Si、Ge等四价元素中掺入
- 述硬磁材料、软磁材料的性能要求及其常用的
- 当不同壁面反射而达到听者的声音所经过的路
- 要获得一束高能激光,请问如何实现?
- 计算下列Ti3+和
- 叙述马西森定律的内容并说明为什么电阻分为
- 设一一维晶格的电子能带可写成:E(k)
- 某种金属的导带底部的有效质量倒数张量为
- 求密排六方结构的几个结构因子?讨论几何消
- 属经塑性形变电阻率增大的原因是什么?
- 何为能带理论?它与近自由电子近似和紧束缚
- 画出恒应力下的应变弛豫和恒应变下的应力弛
- 写出克劳修斯-莫索蒂方程,并论述其物理意
- 什么是粘、滞弹性的静态响应特性?解释恒应
- 铜的晶格常数为0.362nm, 设定一个
- 影响界面结合强度的因素有哪些?