试题详情
- 简答题设总体X的概率密度为
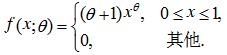，其中Θ＞0为未知参数，X1，X2，…，Xn为来自X的样本，x1，x2，…，xn为相应的样本值。 （1）求Θ的矩估计量； （2）求Θ的最大似然估计量.
关注下方微信公众号，在线模考后查看
热门试题
- 玻璃杯成箱出售，每箱20只，假设各箱含0
- 设随机变量（X，Y）的联合分布密度函数是
- 设A，B为随机事件，=0则（）.
- 在100件产品中有5件是次品，从中不放回
- 设随机变量X～N（2，9），且P{Xa}
- 设总体X~N（μ，42<
- 设某校学生的身高服从正态分布，今从该校某
- 设A、B、C是Ω中的随机事件，将下列事件
- 设总体是来自X的样本，求m，p的矩估计量
- 随机变量X和Y的概率密度分别为 &la
- 设随机变量X服从参数为2的指数分布，则E
- 设A与B互为对立事件，且P（A）>0，P
- 设连续型随机变量X的概率密度函数为f（x
- 以X表示某商店从早晨开始营业起直到第一顾
- 某人下午5：00下班，他所积累的资料表明
- 已知一批机械零件的直径X（单位：mm）服
- 设X~N（1，4），Φ（0.5）=0.6
- 设随机变量X与Y独立，且X，Y的概率密度
- 设F1（x）与F<
- 设为总体的一个样本，则=（）。