试题详情
- 简答题
已知系统的微分方程为：
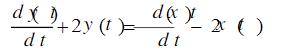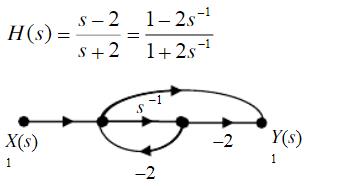
求系统函数H（s），并画出系统的模拟结构框图或信号流图
-
关注下方微信公众号，在线模考后查看
热门试题
- 若Z变换的收敛域是|z|＞Rx
- 用拉氏变换分析法，求系统的响应。
- 描述线性非时变连续系统的数学模型是（）
- 设一系统的输入系统函数试求系统的零状态响
- 已知信号f（t）=ε（t
- 已知信号x（t）的傅里叶变换为X（j&o
- 系统的状态方程和输出方程分别为 （1）
- 离散时间系统，系统函数收敛域∞≥∣z∣＞
- 某连续LTI时间系统得频率响应H（j&o
- 已知信号f（t）的单边拉氏变换是F（s）
- 求图中所示f(jΩ)的傅里叶
- 信号f（t）=ejω·t
- 已知描述某线性时不变因果连续时间系统的微
- 傅里叶变换的对偶性有何意义？
- 计算下列序列的傅里叶变换。 （1）2
- 阶跃信号通过理想低通滤波器，其响应的上升
- 建立如图所示电路的状态方程。若指定输出为
- 已知信号f（2t+2）如图所示，试画出f
- 已知描述某线性时不变因果离散时间系统的差
- 如果一线性时不变系统的单位冲激响应h(t