试题详情
- 简答题设X1，...，Xn为总体X的样本，X的密度函数为
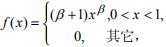其中β>-1为未知参数。试求 （1）β的矩法估计； （2）β的极（最）大似然估计。
关注下方微信公众号，在线模考后查看
热门试题
- 设随机变量X的概率密度为 求（1）系数
- 已知随机向量（X，Y）的联合密度函数则E
- 甲、乙二人轮流投篮，甲先开始，直到有一人
- 设随机变量X和Y相互独立，其概率分布分别
- 设随机变量X～N（2，9），且P{Xa}
- X~N（μ，σ2）
- 设随机变量X和Y的方差分别为25和36，
- 设随机变量X服从e（2），则EX
- 三个人独立地向某一目标进行射击，已知各人
- 设总体X具有概率密度参数θ未
- 设二维随机变量（X，Y）的联合分布律为
- 公共汽车站每隔5分钟有一辆汽车通过．乘客
- 设（X，Y）的联合密度为f（x，y），则
- 利用切比雪夫不等式估计随机变量与其数学期
- 向一目标射击，目标中心为坐标原点，已知命
- 某车间生产的螺钉，其直径X~N（μ，σ<
- 从（0，1）中随机地取两个数，求： （
- 已知事件A、B的概率分别为P（A）=0.
- 已知正常男性成人血液中，每一毫升白细胞数
- 对任意随机变量X，若EX存在，则E[E（