试题详情
- 简答题
某LTI系统的微分方程为：y″（t）+5y′（t）+6y（t）=2f′（t）+6f（t）。已知f（t）=ε（t），
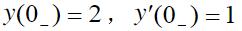求分别求出系统的零输入响应、零状态响应和全响应yzi(t)、yzs(t)和y(t)。
-
关注下方微信公众号，在线模考后查看
热门试题
- 已知=（）
- 一个因果稳定的离散系统，其H（z）的全部
- 某离散系统的系统函数，欲使其稳定的k的取
- 试判定下列系统的稳定性
- 则=（）
- 某离散时间系统的差分方程为，该系统的阶次
- 拉氏变换法既能求解系统的稳态响应，又能求
- 什么是理想低通滤波器？物理上能否实现？为
- 已知某离散系统的差分方程为2y（k）-y
- 求频谱函数的傅立叶反变换。
- 已知系统的响应y（t）与激励f（t）的关
- 某连续LTI时间系统得频率响应H（jω）
- =（） =（） =（） =（）
- 有限长序列f（n）=3δ（n）+2δ（n
- 已知系统的传输算子为，求系统的自然频率为
- 已知某高通的幅频特性和响频特性如图所示，
- 列出如图所示系统的差分方程，已知边界条件
- 对图示信号，求f1
- 强迫响应一定是稳态响应。（）
- 面若已知f1（t）