试题详情
- 简答题 设弹性体内的位移场为
，其中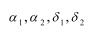
都是与1相比很小的数，试求应变张量、转动角位移矢量及体积膨胀率（相对体变）。
-
关注下方微信公众号，在线模考后查看
热门试题
- 根据达兰贝尔原理，推导弹性介质运动的应力
- 简述非均匀波的主要特点。
- 弹性动力学的基本假设有哪些？
- 解释克其霍夫绕射公式中各项的物理含义，并
- 已知一简谐P波的波函数为，试求以下问题：
- 常见的平面极化波有哪几种？什么叫转换波？
- 什么是正应变、切应变、相对体变？写出它们
- 设弹性体内的位移场为，其中都是与1相比很
- 什么是机械能密度？什么是能流密度？写出能
- 杨氏模量、泊松比、剪切模量、体变模量各表
- 写出能流密度与应力张量和位移矢量的关系。
- 克其霍夫积分解求解的是哪一类波动方程？其
- 已知一弹性介质内，位移场为,其中试求点P
- 写出周期、频率、波长、波数、速度各量之间
- 利用傅里叶变换法求解波动方程一维齐次波动
- 根据虎克定律，推导正应力与正应变关系式，
- 解释波动方程的克其霍夫积分解即式（6—1
- 已知弹性介质中杨氏模量为E，泊松比为，求
- 写出平面P波垂直入射到弹性界面上时的反射
- 写出能流密度与应力张量和位移矢量的关系。