试题详情
- 简答题设一厂商使用的可变要素为劳动L,其生产函数为: Q=-0.01L3+L2+38L 其中,Q为每日产量,L是每日投入的劳动小时数,所有市场(劳动市场及产品市场)都是完全竞争的,单位产品价格为0.10美元,小时工资为5美元,厂商要求利润最大化。问厂商每天要雇用再多少小时劳动?
- 第一,已知工资W=5。
第二,根据生产函数及产品价格P=0.10,可求得劳动的边际产品价值如下(其中,MPL表示劳动的边际产品)
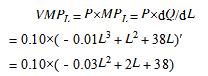
第三,完全竞争厂商的利润最大化要求边际产品价值等于工资,即
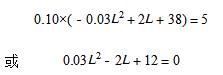
第四,解之得L1=20/3,L2=60。
第五,当L1=20/3时,利润为最小(因为dMPL/dL=1.6>0),故略去。
第六,当L2=60时,利润为最大(dMPL/dL=-1.6<0)。故厂商每天要雇用60小时的劳动。 关注下方微信公众号,在线模考后查看

热门试题
- 依据担保法的规定,下列不能作为保证人的有
- 在具体运用中,农产品支持价格采取可哪两种
- 在现有的资源与技术水平下,表示可能生产的
- 完全竞争和垄断竞争的主要区别是()
- 政府把价格限制在均衡水平以下可能导致()
- 劣质品需求的收入弹性为()。
- 资源配置如果无法做到改善某些人的福利,同
- 如果竞争市场的价格超过(),追求利润最大
- 垄断为什么不能实现资源配置的帕累托最优?
- 下列关于经济租与准租金的论述正确的是()
- 如果无论其他人选择什么策略,某个参与人都
- 对于生产函数Q=f(L,K)和成本方程C
- 当把一定资源用于生产某种产品时()就是这
- 古诺模型假设市场中的各个厂商()。
- 一个厂商增加产量,平均成本从12元上升到
- 某垄断厂商在甲乙两地进行销售,在甲地的边
- 厂商多雇佣一个工人的价值等于()
- 假定效用函数为U=q0.5
- 局部均衡分析方法忽略了市场之间的相互影响
- 假定某企业某年发生隐含成本20万元,明显