试题详情
- 简答题 用古巴比伦人的方法求
 的有理近似值(保留三位小数)。
的有理近似值(保留三位小数)。
-
因为12<3<22,则我们设2为这个根的首次近似。然后进行如下运算:
b1=3÷2=1.5
a2=(1.5+2)÷2=1.75
b2=3÷1.75=1.714
a3=(1.75+1.714)÷2=1.732
得到有理近似数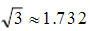
关注下方微信公众号,在线模考后查看

热门试题
- 刘徽的()证明圆面积公式:刘徽说“割之弥
- 古埃及的数学知识常常记载在()。
- 一张渔网,其中的节点数、网眼数与边数这三
- 牛顿创造了现在通用的微分和积分的符号。
- 1906年发现了已经失传的阿基米德的羊皮
- 《周易》中所包含的数学思想有:(1)组合
- 梅文鼎《勾股举隅》中给出了勾股定理的证明
- 关于数学的哲学说是来源于哪个国家()
- 1637年,()发表了他的哲学名著《更好
- 柯朗是()的数学家。
- .古希腊的三大著名几何问题是()、()和
- 对韦达所使用的代数符号进行改进的工作是由
- 刘徽还用无穷小分割和极限方法证明了一条
- 简述微积分先驱数学家的贡献。
- 公元17世纪时,世界上懂得微积分的数学家
- 在进行寻找最优方案的“折纸法”时,一共用
- 《几何原本》传入中国,首先应归功于数学家
- 根据《MathematicalIntel
- 用运动的观点来看对称,平面图形的对称的本
- Wentworth和Smith在1913