试题详情
- 简答题均质细杆长为l,重Q,上端B靠在光滑的墙上,下端A以铰链和圆柱体中心连接,圆柱重P,半径为r,放在粗糙的地面上,由静止开始做只滚不滑的运动,如杆与水平面的夹角θ=45°,求A点在初瞬时的加速度。
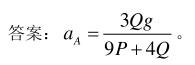
关注下方微信公众号,在线模考后查看

热门试题
- 一动点沿一曲线作匀加速运动,则该点的切向
- 质点系动量矩定理的数字表达式为,则()
- 已知平面平行力系的五个力(图中所示)分别
- 求解空间任意力系的问题在应用投影方程时,
- 已知F1=20kN
- 平面任意力系平衡的必要和充分条件是()
- 试求由质点组的动量矩的笛卡尔分量所组成的
- 外力合力落于摩擦锥以内时不能使物体运动的
- 在空间问题中,力对轴的矩是代数量,而对点
- 刚体转动时角速度等于()对时间的一阶导数
- 一质点从高为处以初速度垂直下落,选轴垂直
- 刚体作平动,其上各点的轨迹相同,均为直线
- 若系统的总动量为零,则系统中每个质点的动
- 无重水平梁的支撑和载荷如图a,b所示,已
- 由AC和CD构成的组合梁通过铰链C连接。
- 图中各个力之间的关系式是()
- 在每一瞬时,作定轴转动的刚体其上各点的角
- 由三个质点组成的质点系,每个质点的质量都
- 均质细长杆质量为m,长度L,匀角速度转动
- 已知:m,l,α,&omeg