试题详情
- 简答题 已知某系统的系统函数为
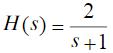，激励信号为x（t）=3cos2t，则该系统的稳态响应为（）
-
关注下方微信公众号，在线模考后查看
热门试题
- 若收敛坐标落于原点，S平面有半平面为收敛
- 设有系统函数为，试求系统的幅频特性和相频
- 绘出下列时间函数的波形图： f
- 已知系统的响应y（t）与激励f（t）的关
- 已知某离散时间系统的输入f（n）和输出y
- 已知描述某线性时不变因果离散时间系统的差
- 信号的频谱是周期的离散谱，则原时间信号为
- 设的收敛域为Re{s}＞-1，&ensp
- 离散时间系统如图所示，已知y（-1）=y
- 若求的表达式，并画出频谱图。
- 将信号f（t）变换为（）称为对信号f（t
- 设有一阶系统方程y′（t）+3y（t）=
- 序列f（k）=-ε（-k）的z变换F（z
- 一离散时间LTI因果系统的差分方程为
- 线性系统响应满足以下规律（）。
- 矩形信号u（t+1）-u（t-1）的傅里
- 系统函数，对应的微分方程为（）
- 已知系统阶跃响应为，为使其响应为，求激励
- 当激励为阶跃信号时，系统的全响应就是阶跃
- 已知离散系统的差分方程则系统的单位样值响