试题详情
- 简答题理想低通滤波器的截止频率选择不恰当时,会有很强的振铃效应。试从原理上解释振铃效应的产生原因。
- 理想低通滤波器(频域)的传递函数为:

滤波器半径交叉部分(侧面图):
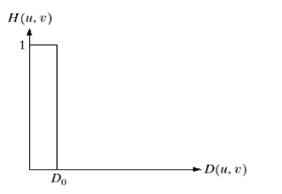
对应空间域(进行傅立叶反变换,为sinc函数):
 用理想低通滤波器滤波时,频域:G(u,v)=F(u,v)H(u,v),傅立叶反变换到时域有:g(x,y)=f(x,y)*h(x,y),频域相乘相当于时域作卷积。因此,图像经过理想低通滤波器后,时域上相当于原始图像与sinc函数卷积,由于sinc函数振荡,则卷积后图像也会振荡;或者说由于sinc函数有两个负边带,卷积后图像信号两侧出现“过冲现象”,而且能量不集中,即产生振铃效应。若截止频率越低,即D0越小,则sinc函数主瓣越大,表现为中心环越宽,相应周围环(旁瓣)越大。而中心环主要决定模糊,旁瓣主要决定振铃效应。因此当介质频率较低时,会产生很强的振铃效应。选择适当的截止频率,会减小振铃效应。
用理想低通滤波器滤波时,频域:G(u,v)=F(u,v)H(u,v),傅立叶反变换到时域有:g(x,y)=f(x,y)*h(x,y),频域相乘相当于时域作卷积。因此,图像经过理想低通滤波器后,时域上相当于原始图像与sinc函数卷积,由于sinc函数振荡,则卷积后图像也会振荡;或者说由于sinc函数有两个负边带,卷积后图像信号两侧出现“过冲现象”,而且能量不集中,即产生振铃效应。若截止频率越低,即D0越小,则sinc函数主瓣越大,表现为中心环越宽,相应周围环(旁瓣)越大。而中心环主要决定模糊,旁瓣主要决定振铃效应。因此当介质频率较低时,会产生很强的振铃效应。选择适当的截止频率,会减小振铃效应。 关注下方微信公众号,在线模考后查看

热门试题
- 数字图像的优点包括()。
- 什么是灰度直方图?它有哪些应用?从灰度直
- 在图像的锐化处理中,通过一阶微分算子和二
- 请将空间坐标变换的两种方法进行比较。
- 形态学处理中最基本的运算是腐蚀与膨胀。其
- 为什么要进行伽马校正,试解释伽马校正的基
- 遥感图像的增强处理包括()等。
- 数字图像处理包含很多方面的研究内容。其中
- 对下图作3×3中值滤波处理,写出处理结果
- 一般来说,直方图均衡化处理对于灰度分布比
- 什么是维纳滤波器?
- 数字图像处理的特点是什么?
- 使用同态滤波方法进行图像增强时,以下处理
- 局部统计法用()和()进行对比度增强。
- 图像量化时,如果量化级比较小会出现什么现
- 均匀指的是()
- 经过细线化之后,图像中所有线条的幅度均为
- 二维傅立叶变换有哪些性质?
- 简述图像几何变换与图像变换的区别。
- 图像频域滤波是先将图像进行二维傅里叶变换