试题详情
- 简答题 设二阶线性定常系统的状态方程为：
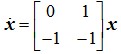试用李雅普诺夫第二法判断该系统平衡点的稳定性。
-
关注下方微信公众号，在线模考后查看
热门试题
- 设系统如图（a）所示，其开环传递函数 要
- 利用李亚普诺夫第一方法判定系统的稳定性。
- 已知受控系统的方程为，请设计状态反馈控制
- 离散系统的状态方程为 （1）是否存在一
- 证明对于线性定常系统的线性变换，其传递函
- 试将下列系统按能观性进行结构分解
- 系统的状态转移矩阵不仅包含了对应自治系统
- 已知系统的传递函数为 （1）采用串联分解
- 已知系统状态方程为： 试设计一状态反馈
- 已知受控系统传递函数为， 综合指标为：&
- 已知系统的状态空间描述如下：其中a、b、
- 使判断下列系统通过状态反馈能否镇定
- 单位反馈系统开环对数幅频特性如右图,试求
- 等价的状态空间模型具有相同的传递函数。
- 试绘制下列开环传递函数的奈奎斯特曲线：
- 设一时滞控制系统如图所示。已知图中的G<
- 设系统的状态空间表达式为 若该系统的状
- 已知系统方程为： （1）求系统的平衡态
- 试将下列系统按能控性和能观性进行结构分解
- 有电路如图所示。以电压u（t）为输入量，