试题详情
- 简答题对f(x)=sinx在[0,π/2]上求1次和3次伯恩斯坦多项式,并与相应的马克劳林级数部分和误差做比较。
-
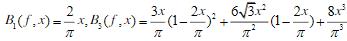
相应的麦克劳林级数分别为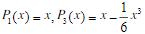 ,
,
部分和误差则为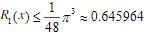 ,
,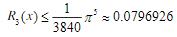 ,
,
大于伯恩斯坦多项式的误差。 关注下方微信公众号,在线模考后查看

热门试题
- 对于f(x)=0的牛顿公式, 证明收敛到
- 解非线性方程f(x)=0的牛顿迭代法具有
- 用高斯-约当方法求A的逆阵:
- 设A∈Rn*n,证
- 设xi(i=0,1
- 试分别用Jacobi迭代法和Gauss-
- 对于一阶微分方程初值问题,取步长h=0.
- 已知近似值xA=2
- 用Romberg方法求,要求误差不超过。
- 用复化Simpson公式计算积分的近似值
- 给定规格化的浮点数系F://β=2,n=
- 已知方程组Ax=b,其中 (1)写出该
- 用Gauss消去法求解下列方程组。
- 正方形的边长大约为100cm,应怎样测量
- 若x=e≈2.71828=x*
- 证明对于任意选择的A,序列收敛于零
- 取5个等距节点 ,分别用复化梯
- 方程组Ax=b,其中,A是对称的且非奇异
- 设方程组 证明解此方程的Jacobi迭
- 用雅可比、高斯-塞德尔迭代法,求解方程组