试题详情
- 简答题甲、乙比赛射击,每进行一次比赛,胜者得一分。在一次射击中,甲“胜”的概率为α,乙“胜”的概率为
 。设
。设 ,规定比赛进行到有一人超过对方2分就停止(各次比赛相互独立),多得2分者胜。求甲获胜的概率。
,规定比赛进行到有一人超过对方2分就停止(各次比赛相互独立),多得2分者胜。求甲获胜的概率。
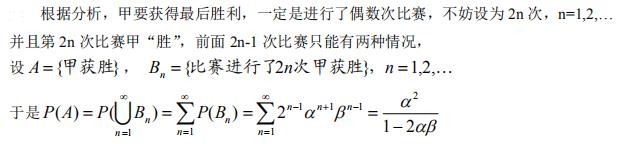
关注下方微信公众号,在线模考后查看

热门试题
- 三个人独立地向某一目标进行射击,已知各人
- 设随机变量X的概率密度为 求: (1)
- 某保险公司把被保险人分为三类:“谨慎的”
- 设随机变量X的分布函数如下: 试填上(
- 设随机变量ξ(ξ>0)。的分
- 有一批建筑房屋用的木柱,其中80%的长度
- 设随机变量X上服从均匀分布,试求随机变量
- 因素A分3个水平,对每个水平进行4次试验
- 已知事件A、B的概率分别为P(A)=0.
- 设X~U[0,1],Y~U[0,1]且X
- 假设随机变量X的概率密度为 现在对X进行
- 从正态总体N(μ,0.5
- 设A,B为两个随机事件,P(A)=0.6
- 甲、乙两人轮流投篮,甲先投。一般来说,甲
- 设ξ,η相互独立且都服从正
- 设X服从参数为1的指数分布,则=().
- 已知随机向量(X,Y)的协方差矩阵V为
- 设随机变量X服从(0,2)上的均匀分布,
- 利用正态分布有关结论,().
- 从数字1,2,…,10中有放回地任取4个