试题详情
- 简答题某种商品每件表面上的疵点数X服从泊松分布,平均每件上有0.8个疵点.若规定表面不超过一个疵点的为一等品,价值十元,表面疵点数大于1不多于4的为二等品,价值8元.某件表面疵点数是4个以上则为废品,求产品价值的均值和方差.
-

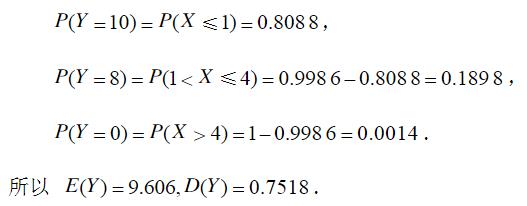
关注下方微信公众号,在线模考后查看

热门试题
- 设随机变量X服从二项分布B(3,0.4)
- 已知随机变量X的概率密度为,则概率P{&
- 设X,Y是相互独立的随机变量,其分布律分
- 设随机变量(X,Y)的分布密度求: (1
- 袋中有N只球,其中的白球数X为一随机变量
- 设随机变量X1,X
- 设(X,Y)的联合概率密度为判断X与Y的
- 设二维随机变量(X,Y)在抛物线y=x
- 设X为随机变量,E(X)=2,D(X)=
- 设X~N(10,0.022
- 对一个五人学习小组考虑生日问题: (1
- 设F1(x)与F<
- 设随机变量X的概率密度f(x)为
- 设离散型随机变量X的概率函数为 问X的
- 设X为随机变量,C是常数,证明D(X)<
- 一袋中有黄球10个,红球6个.&ens
- 已知(X,Y)的概率密度为, 求(1)常
- 设随机变量X1,X
- 某机构有一个9人组成的顾问小组,若每个顾
- 假设总体X~,是来自总体的一个样本,为其