试题详情
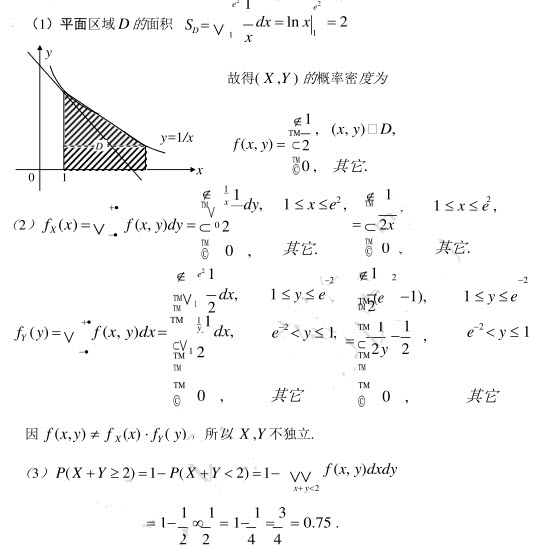
- 简答题设二维随机变量(X,Y)在由曲线y=1/x及直线y=0,x=1,x=e2所围成的平面区域上服从均匀分布。试求: (1)(X,Y)的联合概率密度; (2)求边缘密度fX(x)和fY(y),并说明X与Y是否独立; (3)P(X+Y≥2)。
关注下方微信公众号,在线模考后查看

热门试题
- 设总体为其样本,问:估计量中,哪一个是&
- 袋中有15只白球5只黑球,从中有放回地取
- 设随机变量X的概率密度为求X的分布函数F
- 已知一条昆虫生产n个卵的概率为 设一个
- 设P{X=x1}=
- 对总体参数进行区间估计,则下列结论正确的
- 据数据显示,每1000名50岁的低风险男
- 设总体X服从指数分布 试利用样本X
- 设随机变量X~N(1,22
- 设A,B为随机事件,则下列各式中正确的是
- 设总体X~N(μ,32<
- 设A,B,C为三事件,用A,B,C的运算
- 设(X,Y)的联合概率密度为 (1)求
- 某人忘记了电话号码的最后一个数字,因而他
- 车间中有6名工人在各自独立的工作,已知
- 设随机变量X和Y相互独立,其概率分布分别
- 若随机变量X~N(3,9),Y~N(-1
- 某校高一某班的某次数学测试成绩(满分为1
- 在一标准英语字典中具有55个由二个不相同
- 试验中所有可能出现的基本事件只有有限个,