试题详情
- 简答题 设X（z）是x（n）的Z变换，证明：Z[x（-n）]=X（1/z）。
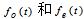分别表示信号f（t）的奇偶分量，证明：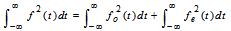
-
直接用Z变换定义证明。
利用奇偶分量与原信号的关系以及奇函数从负无穷到正无穷积分为零来证明。 关注下方微信公众号，在线模考后查看
热门试题
- 求tu（t）*u（t） 已知序列分别求其
- 离散时间系统是指输入、输出都是（）的系统
- e(t)与h(t)的卷积表达式为（）。
- 序列ZT的ROC不是以极点为边界的。
- 拉普拉斯变换是连续时间系统进行分析的一种
- 序列的ZT在其收敛域，即ROC内是解析的
- 所有高于截止频率的频率分量都将不能通过系
- 在没有激励的情况下，系统的响应称为（）。
- 双边序列ZT的ROC是以模的大小相邻的两
- 离散时间系统是指输入、输出都是（）的系统
- 所谓频谱搬移特性是指时间域信号乘一个复指
- 绘出f（t）=u（cost）在（3π，3
- 信号的傅立叶变换存在的充分条件是信号f（
- 在没有激励的情况下，系统的响应称为零输入
- 信号时移只会对幅度谱有影响。
- 信号的时域平移不影响信号的FT的（），但
- （）所有信号都可以用确定的时间函数来描述
- 离散系统的传递函数定义式是：（）。
- 如果x（n）是偶对称序列，则X（z）=X
- 傅立叶变换与傅立叶逆变换的本质是一致的，