试题详情
- 简答题有一个一阶平稳马尔可夫链X1,X2,……Xr……,各Xr取值于集合A={a1,a2,a3}。已知起始概率p(Xr)为p1=1/2,p2=p3=1/4,转移概率如下。
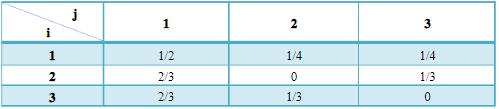 (1)求(X1,X2,X3)的联合熵和平均符号熵。 (2)求这个链的极限平均符号熵。 (3)求H0,H1,H2和它们所对应的冗余度。
(1)求(X1,X2,X3)的联合熵和平均符号熵。 (2)求这个链的极限平均符号熵。 (3)求H0,H1,H2和它们所对应的冗余度。




关注下方微信公众号,在线模考后查看

热门试题
- 设有扰离散信道的传输情况分别如图所示。求
- 连续信源或模拟信号的信源编码的理论基础是
- 设有一个无记忆信源发出符号A和B,已知,
- 已知某线性分组码的最小汉明距离为3,那么
- 率失真函数的值与信源的输入概率无关。
- 考虑一个只取整数值的随机变量X,满足,其
- 下列不属于消息的是()。
- 一副充分洗乱了的牌(含52张牌),试问
- 简述离散信道容量的一般计算方法及其步骤。
- 常用的检纠错方法有()、反馈重发和混合纠
- 简述平均互信息量的性质及理解。
- 设离散无记忆信源S其符号集A={a1,a
- 写出香农公式,并说明其物理意义。当信道带
- 证明离散信源有,并说明等式成立的条件。
- 简述Shannon第二定理(信道编码定理
- 有一信源输出X∈{0,1,2},其概率为
- 简述各种熵(信源熵,条件熵,联合熵(共熵
- 设有二个离散信道,其分别输入为X
- 简述广义的信道编码的分类及各类编码的作用
- m阶马尔可夫信源和消息长度为m的有记忆信