试题详情
简答题系统差分方程为y（n）=3y（n-1）+3y（n-2）-y（n-3）=x（n），用时域分析法求解系统的单位样值响应。
  • 分方程的特征方程为：
    特征根为：a1=a2=a3=1即为三重根
    方程齐次解为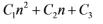
    因为系统起始时静止，可知h（-2）=h（-1）=0，h（0）=δ（0）=1。
    所以，h（0）=1，h（-1）=0，h（-2）=0。
    将h（0），h（-1），h（-2）代入差分方程可得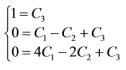
    解得C1=1/2，C2=3/2，C3=1
    系统的单位样值响应为：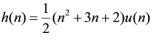

  • 关注下方微信公众号，在线模考后查看

热门试题