试题详情
- 简答题 已知弹性体内部某点的应力张量为
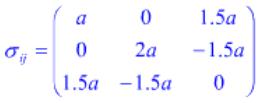试将上述应力张量分解为应力球张量和应力偏张量，并求解应力偏张量的第二不变量。
-
关注下方微信公众号，在线模考后查看
热门试题
- 矩形薄板的边长分别为a和b，四边简支，薄
- 进行直梁有限元分析，平面刚架单元上每个节
- 均匀性假定是指整个物体的体积都被组成这个
- 把经过物体内任意一点各个（）上的应力状况
- 悬臂梁在自由端承受集中力F和弯矩M的作用
- 切应力互等定理根据条件（）成立。
- 关于弹性力学平面问题的极坐标解，下列说法
- 简述整体坐标的概念。
- 边界条件表示在边界上（）与（），或（）与
- 试证能满足相容方程，并考察它在下图所示矩
- 设有矩形截面的悬臂梁，在自由端受有集中荷
- 试述求整体刚度矩阵的两种方法。
- 试分析说明，在不受任何面力作用的空间体表
- 在常体力，全部为应力边界条件和单连体的条
- 在下图的微分体中，若将对形心的力矩平很条
- 证明应力函数φ=by²
- 弹性力学的基本假设是什么。
- 试述弹性力学研究方法的特点，并比较材料力
- 已知复位势函数φf
- 已知半径为b的圆板，在圆板中心有一个能够