试题详情
- 简答题 悬臂梁在自由端承受集中力F和弯矩M的作用,如图所示。设跨度为l,抗弯刚度为EI。试用最小势能原理求解以挠度表示的平衡微分方程及边界条件。
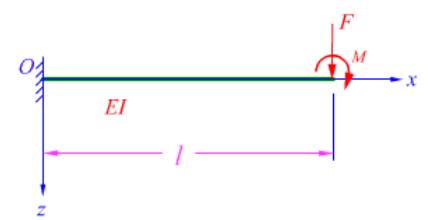
-
关注下方微信公众号,在线模考后查看

热门试题
- 证明应力函数φ=by2
- 直角三角形固定在刚性基础上,受齐顶的水压
- 如图所示,悬臂梁上部受线性分布荷载,梁的
- 试利用拉梅弹性常数λ和G表示弹性模量E,
- 简支梁跨度为l,承受均布载荷q的作用,抗
- 圆形薄板,半径为a,边界筒支,受均布荷载
- 考虑上端固定,下端自由的一维杆件,见图,
- 悬臂梁在自由端承受集中力F和弯矩M的作用
- 已知长半轴为a,短半轴为b的椭圆形截面杆
- 下图中的有限单元划分,哪种图示的单元划分
- 试举例说明什么是均匀的各向异性体,什么是
- 在平面三结点三角形单元的公共边界上应变和
- 已知应力分量,判断该应力分量是否满足平衡
- 有限元法有哪些优缺点?
- 试证明应力函数ϕ=M&thet
- 在选择多项式位移模式的阶次时,要求所选的
- 有限元法中等参数单元的主要优点是什么?
- 三角形单元的位移模式为()
- 平面问题中划分单元的数目是否越多越好?
- 结构的网格划分应注意哪些问题.如何对其进