试题详情
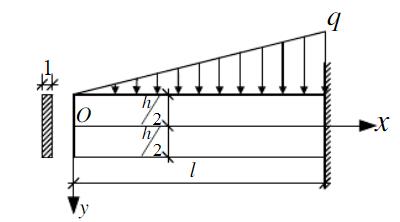
- 简答题 如图所示,悬臂梁上部受线性分布荷载,梁的厚度为1,不计体力。试利用材料力学知识写出σx,τxy表达式;并利用平面问题的平衡微分方程导出σy,τxy表达式。
-

关注下方微信公众号,在线模考后查看

热门试题
- 弹性力学中,正面是指()的面,负面是指(
- 矩形截面的柱体受到顶部的集中力和力矩M的
- 作用均匀分布载荷q的矩形横截面简支梁,如
- 已知如图所示的三角形单元,设其厚度为t,
- 证明应力函数φ=by2
- 边界条件表示边界(),或()之间的关系式
- 试比较弹性力学和材料力学中关于切应力的符
- 已知应力分量 判断该应力分量是否满足平
- 已知悬臂梁如图所示,如果悬臂梁的弯曲正应
- 试述街节点力和节点载荷的区别。
- 有限元是近似求解()问题的数值方法。
- 平面刚架结构在外力的作用下,横截面上的内
- 已知两组位移分量分别为 其中a
- 结构的网格划分应注意哪些问题.如何对其进
- 连续性假定是指整个物体是由同一材料组成的
- 诉述有限元法的定义。
- 在下图中,试导出无面力作用时AB边界上的
- 已知弹性体内部某点的应力张量为 试将上
- 考虑上端固定,下端自由的一维杆件,见图,
- 下列关于应力解法的说法正确的是()。