试题详情
- 简答题证明一个离散信源在它的输出符号等概率的情况下其熵达到最大值。
-
若二元离散信源的统计特性为
P=Q=1,H(X)=-[P*log(P)+(1-P)*log(1-P)]
对H(X)求导求极值,由dH(X)/d(P)=0可得

可知当概率P=Q=1/2时,有信源熵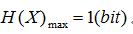
对于三元离散信源,当概率 时,信源熵
时,信源熵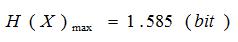
此结论可以推广到N元的离散信源。 关注下方微信公众号,在线模考后查看

热门试题
- 为了传输一个由字母A、B、C、D组成的符
- 对于均值为0,平均功率受限的连续信源,信
- N维连续型随机序列X1X2...XN,有
- 设多项式 为GF(2)上分组长
- 简述广义的信道编码的分类及各类编码的作用
- 每帧电视图像可以认为是由3×10
- 简述信息论的起源、历史与发展。
- 考虑GF(2)上的下列生成矩阵
- 对于限峰值功率的N维连续信源,当概率密度
- 根据输入输出信号的特点,可将信道分成离散
- 设信道输入端的熵为H(X),输出端的熵为
- 每帧电视图像可以认为是由3×10
- 黑白传真机的消息元只有黑色和白色两种,即
- 在连续信源中,根据差熵、条件差熵和联合
- 有一信源发出恒定宽度,但不同幅度的脉冲,
- 假设N个人及组想用保密密钥密码。组中的每
- 不可能事件的自信息量是()。
- 简述卷积码的基本概念和描述方法、编码器构
- 当随即变量X和Y相互独立时,条件熵等于信
- 连续随机变量X和Y的联合概率密度为:,求