试题详情
- 简答题 在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1)h(X|Y)≤h(X),当且仅当X和Y统计独立时等号成立; (2)h(X1X2...XN)≤h(X1)+h(X2)+h(XN),当且仅当X1X2...XN彼此统计独立时等式成立。
-

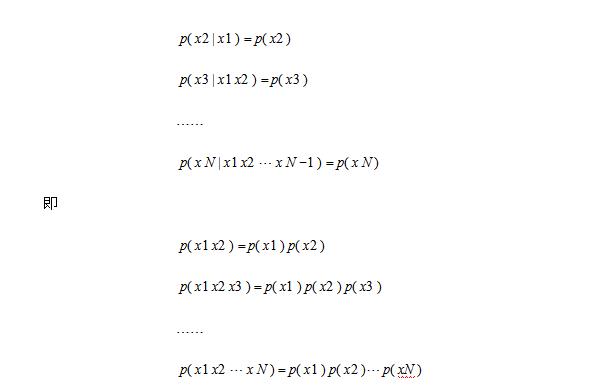
关注下方微信公众号,在线模考后查看

热门试题
- 考虑下图所示的二元编码器。 给出
- 信源空间为: 码符号为X={0,1,2
- 下面哪一项不属于熵的性质:()
- 什么是自信息量?
- 考虑GF(2)上的下列生成矩阵
- 离散无记忆序列信源中平均每个符号的符号熵
- 简述香农第一编码定理的物理意义?
- 试证明H(X)是输入概率分布P(x)的上
- 设多项式 为GF(2)上分组长
- 四进制、八进制脉冲所含信息量分别是二进制
- 设信源通过一干扰信道,接收符号为Y={b
- 简述香农公式的含义。
- 简述Shannon第二定理(信道编码定理
- 为提高通信系统传输消息有效性,信源编码采
- 率失真函数对允许的平均失真度是()。
- N维统计独立均匀分布连续信源的熵是N维区
- 有一个一阶平稳马尔可夫链X1<
- 一个随机事件发生某一结果后所带来的信息量
- 居住某地区的女孩中有25%是大学生,在女
- 设加性高斯白噪声信道中,信道带宽3kHz