试题详情
- 简答题 设信源
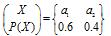 通过一干扰信道,接收符号为Y={b1,b2},信道传递矩阵为
通过一干扰信道,接收符号为Y={b1,b2},信道传递矩阵为 ,求 (1)信源X中事件a1和a2分别含有的自信息量。 (2)收到消息bj(j=1,2)后,获得的关于ai(i=1,2)的信息量。 (3)信源X和信宿Y的信息熵。 (4)信道疑义度H(X/Y)和噪声熵H(Y/X)。 (5)接收到信息Y后获得的平均互信息量。
,求 (1)信源X中事件a1和a2分别含有的自信息量。 (2)收到消息bj(j=1,2)后,获得的关于ai(i=1,2)的信息量。 (3)信源X和信宿Y的信息熵。 (4)信道疑义度H(X/Y)和噪声熵H(Y/X)。 (5)接收到信息Y后获得的平均互信息量。
-

关注下方微信公众号,在线模考后查看

热门试题
- 设二元对称信道的传递矩阵为 (1)若P
- 设有扰离散信道的传输情况分别如图所示。求
- 已知(8,5)线性分组码的生成矩阵为
- 线性码一定包含全零码。
- 考虑下图所示的二元编码器。 给出
- 同时扔一对均匀的骰子,当得知“两骰子面朝
- 求下图中信道的信道容量及其最佳的输入概率
- 算术编码是一种无失真的分组信源编码,其基
- 如果信源和失真度一定,则平均失真度是()
- 有一离散无记忆信源,其输出为X&isin
- 在有扰离散信道上传输符号0和1,在传输过
- 简述消息、信号、信息的含义、定义及区别。
- 事物的不确定度是用时间统计发生()来描述
- 考虑GF(2)上的下列生成矩阵
- 请给出平均码长界定定理及其物理意义。
- 证明离散平稳信源有,试说明等式成立的条件
- 每帧电视图像可以认为是由3×10
- 消息(或称为符号)
- 把n个二元对称信道串接起来,每个二元对称
- 考虑另一个几何分布的随机变量X,满足P(