试题详情
简答题 已知（8，5）线性分组码的生成矩阵为 （1）证明该码为循环码； （2）求该码的生成多项式g（x），一致校验多项式h（x）和最小码距d。
  • （1）生成矩阵作初等行变换：第5行加到第4行，第4行加到第3行，第3行加到第2行，第2行和第5行加到第1行。得

    （2）生成多项式为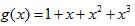，一致校验多项式为

    一致校验矩阵为

    该矩阵的任意1列线性无关，但存在某2列线性相关，故最小码距为2。

  • 关注下方微信公众号，在线模考后查看

热门试题